Top 10 Cons & Disadvantages of Poisson Distribution

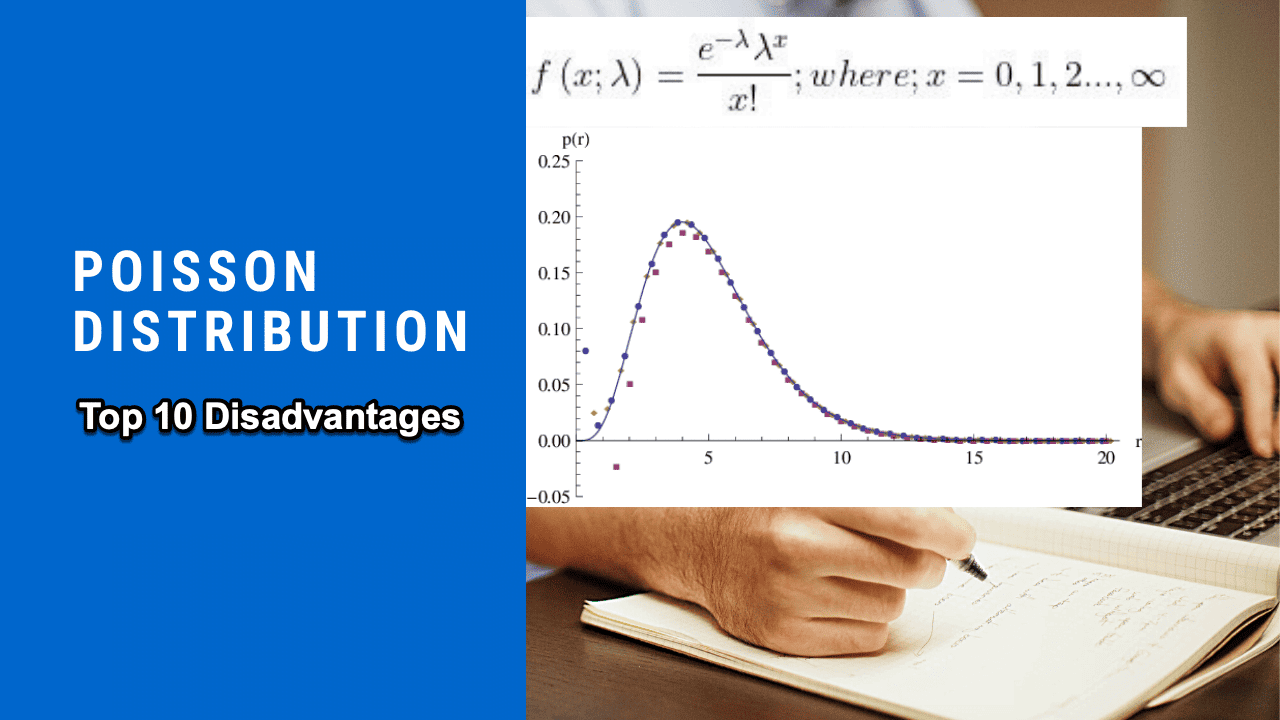
Poisson distribution, a fundamental concept in probability theory and statistics, is widely used to model the number of times an event occurs within a fixed interval of time or space. This distribution is particularly applicable in fields like quantum physics, finance, and various business and engineering aspects. It holds a unique place in statistical methodologies due to its specific properties and assumptions, such as the independence of events and the consistency of the average rate at which events occur. However, Poisson Distribution has limitations like any statistical model and is not a one-size-fits-all solution.

Understanding these limitations is crucial for statisticians, scientists, and business analysts to avoid misinterpretation of data and ensure accurate predictions. While powerful in many contexts, Poisson Distribution can lead to significant inaccuracies if its assumptions and conditions are unmet. The following exploration delves into the top disadvantages of Poisson Distribution, revealing the challenges and complexities of relying solely on this model. This understanding is essential for anyone looking to apply Poisson Distribution in real-world scenarios, ensuring a balanced and critical approach to data analysis.

Top 10 Cons & Disadvantages of Poisson Distribution

When delving into the realm of statistics, the utilization of Poisson Distribution is often met with enthusiasm due to its perceived simplicity and broad applications. However, the reliance on this distribution comes with its own set of challenges. In the following sections, we will explore the top 10 disadvantages of Poisson Distribution.

Each point is not only a numerical drawback but a gateway to understanding the deeper complexities and nuances of statistical modeling. These disadvantages highlight the need for caution and discernment in applying Poisson Distribution, prompting a reevaluation of its suitability in various statistical scenarios.

1. Assumption of Independence

Poisson Distribution’s fundamental assumption of the independence of events is one significant drawback. This model presupposes that the occurrence of one event does not influence the likelihood of another occurring. In real-world scenarios, this is often not the case. For example, in traffic flow analysis, one vehicle passing a point might increase the likelihood of another following closely, especially during peak hours. This interdependence can skew the accuracy of Poisson Distribution, leading to erroneous conclusions. Analysts must recognize that in many practical situations, the interconnectedness of events can make Poisson Distribution an unreliable predictor, demanding alternative approaches that account for potential dependencies.

2. Fixed Interval Limitation

Poisson Distribution requires a fixed interval of time or space for its application, a condition that is not always practical or realistic. In many cases, the intervals of observation are not constant. For instance, in customer service scenarios, the arrival rate of customers can vary significantly, not conforming to the fixed interval assumption. This variability can lead to substantial discrepancies in the model’s predictions, rendering it less effective. Analysts must be wary of applying Poisson Distribution when the observation intervals are irregular or subject to significant fluctuation.

3. Rare Event Focus

The distribution is primarily tailored for modeling rare events, which can be a significant limitation. Poisson Distribution may not be the most appropriate tool in contexts where events occur frequently. For example, in analyzing website traffic for a popular website, the high frequency of visits may not fit well within the framework of Poisson Distribution, as it is designed to model events that occur at a lower rate. Analysts must carefully evaluate the frequency of the events they are studying to determine if Poisson Distribution is the right choice.

4. Overdispersion Issues

Poisson Distribution can struggle with overdispersion – a scenario where the observed variance is higher than the mean. This mismatch is a common issue in real-world data, where the assumption that the mean and variance are equal (as Poisson Distribution requires) does not hold. In such cases, using Poisson Distribution can lead to underestimating the variability in the data, leading to inaccurate conclusions. Analysts must assess their data for overdispersion and consider alternative models like the Negative Binomial Distribution.

5. Underlying Rate Consistency

Poisson Distribution assumes a consistent rate of occurrence for events, which is often not reflective of real-world scenarios. In many cases, the rate at which events occur can fluctuate due to various factors. For instance, in retail, the rate of customer arrivals can vary significantly due to time of day, promotions, or seasonal trends. When the event rate is not constant, the predictions made by Poisson Distribution can be significantly off, limiting its effectiveness.

6. Simplistic Nature

The simplistic nature of Poisson Distribution can be a drawback in complex scenarios. It provides a basic model that does not account for the multifaceted aspects of real-world events. For instance, in healthcare, certain diseases might be influenced by genetics, environment, and lifestyle. The simplicity of Poisson Distribution means it might not capture these complexities adequately, leading to oversimplified and potentially misleading models.

7. Ignoring Larger Context

Poisson Distribution focuses narrowly on the event count within a specified interval, often ignoring the larger context. This narrow focus can lead to overlooking broader trends or patterns crucial for accurate analysis. For example, in environmental studies, while Poisson Distribution can count the number of certain events, it may not account for underlying environmental changes or broader ecological systems that influence these events.

8. Difficulty in Estimating Rate Parameter

Estimating the rate parameter (λ) in Poisson Distribution can be challenging, particularly when data is limited or events are extremely rare. This difficulty can lead to inaccuracies in the model, as the entire distribution hinges on the correct estimation of this parameter. In some fields, such as rare disease occurrences or uncommon natural phenomena, the scarcity of data can estimate λ highly speculative.

9. Not Suitable for Large-Scale Data

Poisson Distribution may not be the best fit for large-scale data sets. In cases where data is extensive and complex, the distribution may fail to capture the nuances and intricate patterns present in the data. For instance, in big data applications, data’s sheer volume and complexity can render Poisson Distribution too simplistic, necessitating more sophisticated statistical models that can handle large-scale data more effectively.

10. Exclusively Discrete Outcomes

A critical limitation of Poisson Distribution lies in its exclusive applicability to discrete outcomes. This distribution is designed to model the count of events, restricting its use to scenarios where outcomes are quantifiable in whole numbers. This characteristic significantly narrows its scope, particularly in fields where data is continuous or non-integer. For instance, in financial markets or scientific measurements, variables often take continuous values, such as prices or measurements that can have fractions or decimals. In these cases, the discrete nature of Poisson Distribution renders it inadequate, as it cannot account for the subtleties and nuances of continuous data.

Understanding Poisson Distribution

Poisson Distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space, assuming that these events occur with a known constant mean rate and independently of the time since the last event. It’s named after the French mathematician Siméon Denis Poisson and is characterized by its parameter λ (lambda), which is the average number of events in the given interval. This distribution is commonly used for modeling count data and rare events in various fields, such as business, engineering, and natural sciences. However, its applicability is subject to specific conditions like the homogeneity of the event rate and the independence of occurrences, which can limit its use in real-world situations where these assumptions do not hold.

Poisson Distribution Studies

• Poisson distribution by ScienceDirect.com
• Poisson distribution by Wikipedia.org
• An Extension of the Poisson Distribution: Features and Application for Medical Data Modeling

Recommended articles from us: Poisson Distribution: 5 Use Cases with 5 Advantages and Top 5 Best Poisson Distribution Calculators

Conclusion

In conclusion, while Poisson Distribution is a powerful tool in statistical analysis, its limitations cannot be overlooked. The ten disadvantages outlined in this article serve as a critical reminder that statistical models, including Poisson Distribution, have specific conditions and assumptions that must be met to provide accurate and reliable results. Misapplication or over-reliance on this distribution can lead to erroneous conclusions and poor decision-making.

As we’ve seen, the effective use of Poisson Distribution requires a deep understanding of its constraints and appropriate contexts. This awareness is vital for statisticians, researchers, and data analysts who seek to apply statistical models in practical situations. In the quest for precision and accuracy in data analysis, recognizing the limitations of our tools is just as important as understanding their strengths. With all its advantages and disadvantages, Poisson Distribution remains a fundamental part of the statistical toolkit. Still, its application must be tempered with critical evaluation and understanding the underlying assumptions.