Poisson Distribution: 5 Advantages with 5 Use Cases
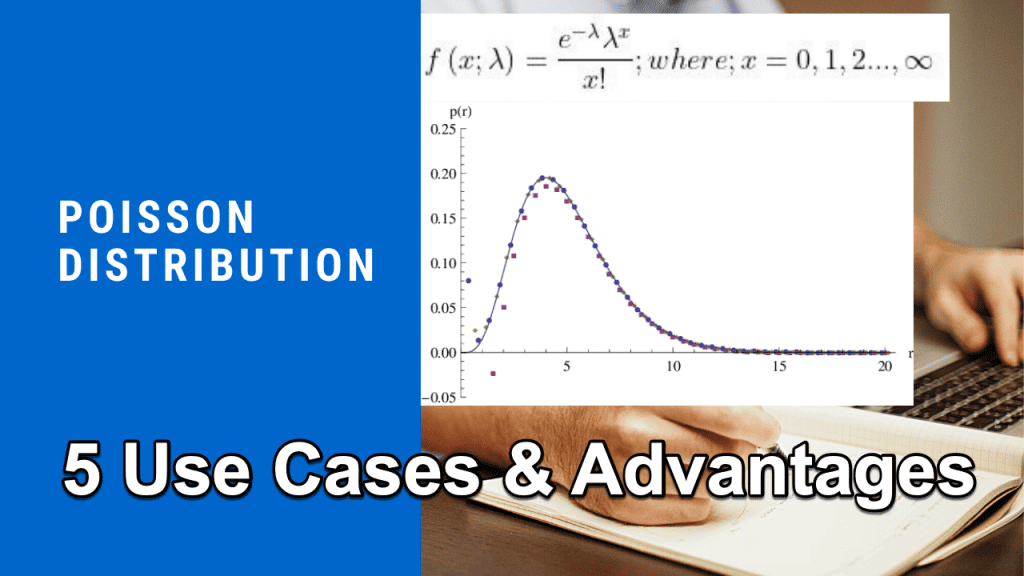
The Poisson distribution is a profound statistical tool used in various fields to model the number of times an event occurs within a fixed interval of time or space. This distribution is particularly valuable when dealing with rare events in large populations or over long periods. It is named after French mathematician Siméon Denis Poisson and is a cornerstone in modern probability theory. Its simplicity and broad applicability make it a fundamental resource for researchers and professionals, offering insights into phenomena that follow a random process.
At its core, the Poisson distribution assumes events occur independently, and the average rate at which they occur remains constant over time. This makes it an ideal model for studying discrete events, particularly in contexts where precision and reliability are crucial. From measuring the frequency of natural occurrences to forecasting business-related activities, the Poisson distribution provides a framework for understanding and predicting the behavior of various systems. Its relevance across different sectors underscores its versatility, making it a versatile tool for statistical analysis.
Poisson Distribution Top 5 Pros & Advantages
The Poisson distribution offers a spectrum of advantages that elevate its status in statistical analysis. Its versatility, simplicity, predictive power, precision in rare event modeling, and efficiency in handling large data sets stand as its cardinal strengths. These attributes make the Poisson distribution a preferred choice among professionals and underscore its significance in a wide range of practical applications. Each advantage illustrates the distribution’s ability to dissect complex phenomena and provide reliable, actionable insights, solidifying its position as a fundamental tool in theoretical and applied statistics.
1. Versatility Across Fields
The Poisson distribution is not confined to a single domain; its versatility allows it to be applied across various fields, from physics to finance and biology to engineering. This adaptability is rooted in its fundamental principle of modeling discrete events, a common element in numerous scenarios. Whether it’s tracking the number of mutations in a DNA sequence, forecasting financial transactions, or monitoring traffic flow, the Poisson distribution provides a consistent framework. This universality demonstrates its applicability and encourages interdisciplinary collaboration, leading to innovative solutions and a deeper understanding of complex systems.
2. Simplified Approach to Complex Problems
In a world where complexity often overwhelms clarity, the Poisson distribution offers a refreshingly simple approach to tackling intricate problems. Its elegance lies in its ability to distill vast, chaotic datasets into manageable models without losing essential information. This simplicity does not compromise depth; instead, it allows for a more intuitive understanding of the data, making it accessible to a wider range of users, not just expert statisticians. By democratizing data analysis, the Poisson distribution empowers more professionals to make informed decisions, fostering a data-driven culture across various sectors.
3. Predictive Power and Planning
Forecasting and planning are critical to successful business, science, and public policy strategies. The Poisson distribution excels in this arena with its robust predictive power. Analyzing historical data can accurately forecast future occurrences of discrete events, enabling organizations to anticipate and prepare for various scenarios. This predictive capacity is invaluable in resource allocation, risk management, and strategic planning, ensuring that reactive, proactive, and evidence-based decisions are made. The Poisson distribution thus becomes an essential tool in shaping future outcomes through informed, data-driven strategies.
4. Precision in Rare Event Modeling
Modeling rare events is a significant challenge in statistical analysis, yet it is crucial for risk assessment and management. The Poisson distribution is particularly adept at accurately representing these low-probability occurrences. In fields like insurance, public health, and safety engineering, where understanding the likelihood of rare but impactful events is essential, the Poisson distribution provides a reliable framework. Its precision in these contexts helps develop effective prevention and mitigation strategies, enhance safety, and reduce potential losses, proving its indispensability in critical decision-making processes.
5. Efficiency with Large Data Sets
In the era of big data, the ability to efficiently process and analyze large volumes of information is paramount. The Poisson distribution meets this challenge with its compatibility with computerized analysis and large data sets. Its efficiency in handling and interpreting vast amounts of data makes it a vital tool in sectors where data is continuously generated at a high volume, such as telecommunications, e-commerce, and social media analytics. This efficiency saves time and resources and ensures that insights are timely and relevant, making the Poisson distribution a key ally in navigating the complexities of the digital age.
Poisson Distribution Top 5 Use Cases
The Poisson distribution is a versatile tool that seamlessly integrates into numerous practical applications. Its utility spans diverse fields, demonstrating its capability to address complex real-world problems. This statistical model excels in situations involving random, independent events, particularly where consistency and precision are paramount. The Poisson distribution proves its indispensability from optimizing traffic flow and enhancing call center efficiency to revolutionizing inventory management, improving manufacturing quality control, and informing healthcare strategies. Each use case exemplifies its power to transform raw data into actionable insights, showcasing its multifaceted role in contemporary analysis and decision-making.
1. Traffic Flow Analysis
The analysis of traffic flow is a quintessential application of the Poisson distribution. It helps estimate the number of vehicles passing through a checkpoint or intersection at a given time. This application is crucial for urban planning and managing traffic congestion.
Real-life Example: Urban planners use the Poisson distribution to predict traffic patterns during peak hours in a busy city. By analyzing historical data, they can forecast the frequency of cars passing a certain point, aiding in traffic light timing adjustments and road infrastructure development to mitigate congestion.
2. Call Center Management
Call centers frequently utilize the Poisson distribution to manage incoming call traffic. This helps in workforce planning and ensuring customer satisfaction by minimizing waiting times.
Real-life Example: A customer service center for a large telecommunications company uses the Poisson distribution to predict the number of incoming calls per hour. This enables them to staff appropriately, ensuring enough agents can handle peak times without excessive customer waiting.
3. Inventory Management
In inventory management, the Poisson distribution is used to forecast product demand. This is essential for maintaining optimal stock levels, reducing holding costs, and avoiding stockouts.
Real-life Example: A retail store uses the Poisson distribution to estimate the daily demand for a popular product. By understanding the likely number of sales per day, the store can maintain an ideal inventory level, balancing between overstocking and running out of items.
4. Quality Control in Manufacturing
In manufacturing, the Poisson distribution helps in quality control by predicting the number of defects or failures in a batch of products. This is crucial for maintaining product quality standards and operational efficiency.
Real-life Example: An electronics manufacturer applies the Poisson distribution to predict the occurrence of defective units in a production run. By estimating the average number of defects, they can refine their manufacturing process and improve quality control measures, ultimately enhancing product reliability.
5. Healthcare and Epidemiology
The Poisson distribution is widely used in healthcare and epidemiology to model the occurrence of rare diseases or the spread of infections within a population.
Real-life Example: Public health officials use the Poisson distribution to estimate the annual number of cases of a rare disease in a given population. This aids in resource allocation, preventive measures, and understanding the disease’s spread patterns.
Poisson Distribution External References
- Understanding Poisson Distribution: A Comprehensive Guide For Statistical Analysis
- Poisson Distribution: Definition & Uses
- Poisson Distribution by ScienceDirect
- Poisson Distribution by Wikipedia.org
Recommended articles from us: Top 10 Cons & Disadvantages of Poisson Distribution and Top 5 Best Poisson Distribution Calculators
Poisson Distribution Video
Conclusion
The Poisson distribution stands as a paragon of statistical elegance and practicality. Its applications, stretching across myriad fields, demonstrate its unique ability to turn complex, random events into comprehensible, manageable models. This distribution is not just a mathematical concept but a powerful tool that drives decision-making, informs strategies, and enhances understanding in various sectors. Its advantages – versatility, simplicity, predictive power, precision in rare event modeling, and efficiency in handling large data sets – are not just theoretical strengths but real-world assets. These attributes enable organizations and individuals to navigate the complexities of their respective fields with greater confidence and insight.
In an era increasingly reliant on data, the Poisson distribution emerges as a critical ally. Whether it’s in managing resources, predicting trends, ensuring quality, or preparing for the unexpected, this distribution provides a solid foundation for evidence-based decision-making. Its role in shaping policies, optimizing operations, and advancing scientific knowledge underscores its enduring relevance. As we face new challenges and explore uncharted territories, the Poisson distribution will remain a key instrument in our statistical arsenal, guiding us toward more informed and effective solutions.

