Poisson distribution, a fundamental concept in probability theory and statistics, is widely used to model the number of times an event occurs within a fixed interval of time or space. This distribution is particularly applicable in fields like quantum physics, finance, and various business and engineering aspects. It holds a unique place in statistical methodologies due to its specific properties and assumptions, such as the independence of events and the consistency of the average rate at which events occur.
However, like any statistical model, Poisson Distribution has limitations and is not a one-size-fits-all solution, requiring careful consideration before application.
Understanding Poisson Distribution
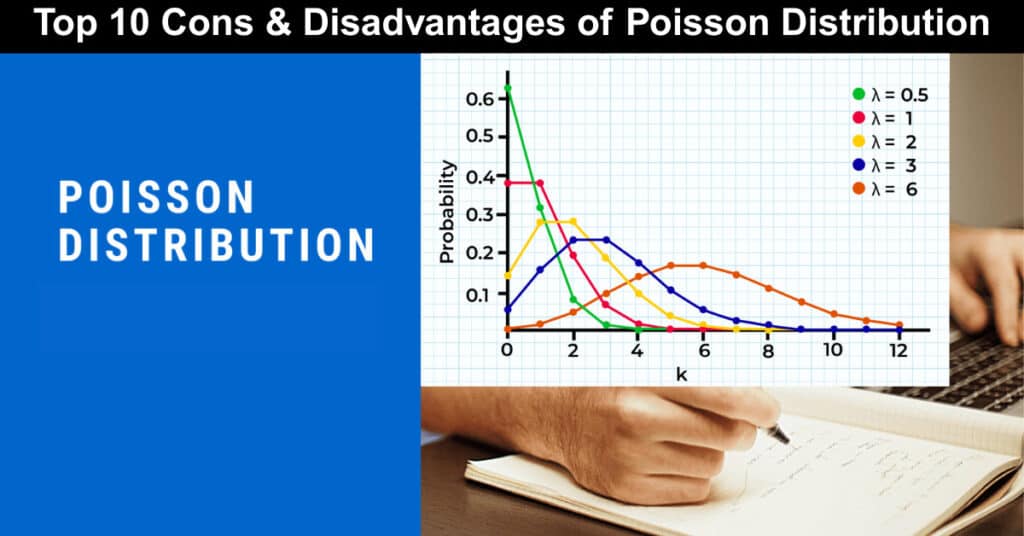
Poisson Distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space, assuming that these events occur with a known constant mean rate and independently of the time since the last event. It’s named after the French mathematician Siméon Denis Poisson and is characterized by its parameter λ (lambda), which is the average number of events in the given interval.
This distribution is commonly used for modeling count data and rare events in various fields, such as business, engineering, and natural sciences. However, its applicability is subject to specific conditions like the homogeneity of the event rate and the independence of occurrences, which can limit its use in real-world situations where these assumptions do not hold.
Top 10 Cons & Disadvantages of Poisson Distribution
When delving into the realm of statistics, the utilization of Poisson Distribution is often met with enthusiasm due to its perceived simplicity and broad applications. However, the reliance on this distribution comes with its own set of challenges. In the following sections, we will explore the top 10 disadvantages of Poisson Distribution. Each point is not only a numerical drawback but a gateway to understanding the deeper complexities and nuances of statistical modeling.
1. Assumption of Independence
The foundational assumption of event independence in Poisson Distribution is a critical limitation. This model presumes that each event occurs without influencing the probability of another. However, many real-world phenomena exhibit inherent dependencies, making this assumption flawed. This can lead to significant modeling errors and inaccurate predictions, challenging the reliability of the Poisson model in interconnected systems where one event’s occurrence directly impacts others.
This core issue manifests in several key ways:
- Violation of Independence: The model presumes events are independent, but in reality, one event can often trigger or prevent another, invalidating this core assumption and leading to flawed statistical conclusions about the data being observed.
- Inaccurate Predictions: When events are dependent, using Poisson Distribution leads to inaccurate probability estimates, as the model fails to capture the true underlying dynamics of the event sequence being analyzed.
Real-Life Example: In traffic flow analysis, one car passing a point often increases the likelihood of another following closely, especially during rush hour. This clustering effect violates the independence assumption. Applying Poisson Distribution here would inaccurately model traffic patterns, potentially leading to poor infrastructure planning and congestion management strategies.
2. Fixed Interval Limitation
Poisson Distribution requires a fixed interval of time or space for its application, a condition that is not always practical or realistic. In many cases, the intervals of observation are not constant. This variability can lead to substantial discrepancies in the model’s predictions, rendering it less effective. Analysts must be wary of applying Poisson Distribution when the observation intervals are irregular or subject to significant fluctuation.
This limitation creates practical challenges in the application of the Poisson process:
- Inflexible Observation Window: The model necessitates a constant interval for event counting, which is often impractical in dynamic environments where observation periods naturally vary or cannot be standardized.
- Data Misrepresentation: Forcing variable-interval data into a fixed-interval model can distort the underlying event rate, leading to misrepresentation of the true statistical properties of the process being studied.
Real-Life Example: In a customer service center, call arrivals fluctuate dramatically throughout the day. Applying Poisson Distribution with a fixed hourly interval fails to capture these variations. This leads to inaccurate staffing models, as the model cannot predict peak and off-peak hours effectively, resulting in either overstaffing or poor customer service.
3. Rare Event Focus
The distribution is primarily tailored for modeling rare events, which can be a significant limitation. Poisson Distribution may not be the most appropriate tool in contexts where events occur frequently. Analysts must carefully evaluate the frequency of the events they are studying to determine if Poisson Distribution is the right choice. Using it for common events can lead to poor model fit and unreliable results.
This focus on rare events presents distinct modeling problems:
- Inapplicability to Frequent Events: The distribution is designed for low-frequency occurrences. When applied to frequent events, the model fails to accurately represent the data’s distribution, leading to significant analytical errors.
- Poor Fit for High-Rate Data: For events with a high occurrence rate, the Poisson model’s shape does not match the data’s pattern, making it an unsuitable and misleading choice for analysis and prediction.
Real-Life Example: Analyzing website traffic for a major e-commerce site like Amazon during a Black Friday sale is unsuitable for Poisson Distribution. The event (page visits) is extremely frequent. Using this model would severely underestimate the volume and variability of traffic, leading to server crashes and a poor user experience.
4. Overdispersion Issues
Poisson Distribution can struggle with overdispersion – a scenario where the observed variance is higher than the mean. This mismatch is a common issue in real-world data, where the assumption that the mean and variance are equal does not hold. In such cases, using Poisson Distribution can lead to underestimating the variability in the data, leading to inaccurate conclusions and potentially flawed decision-making based on the model’s output.
This issue with variance leads to significant analytical shortcomings:
- Mean-Variance Equality Flaw: The model assumes the mean and variance of the data are equal, a condition rarely met in practice, causing a fundamental mismatch between the model and the actual data’s structure.
- Underestimation of Variability: In cases of overdispersion, the Poisson model significantly underestimates the true variance, leading to overconfident predictions and narrow confidence intervals that do not reflect the real uncertainty.
Real-Life Example: In modeling the number of insurance claims within a population, some policyholders may be prone to more claims than others. This creates overdispersion. A Poisson model would underestimate the variability, leading to inadequate reserve funds and potential insolvency for the insurance company due to unexpected claim surges.
5. Underlying Rate Consistency
Poisson Distribution assumes a consistent rate of occurrence for events, which is often not reflective of real-world scenarios. In many cases, the rate at which events occur can fluctuate due to various factors. When the event rate is not constant, the predictions made by Poisson Distribution can be significantly off, limiting its effectiveness and making it an unreliable tool for modeling processes with non-stationary rates.
This assumption of a constant rate is a major practical constraint:
- Static Rate Assumption: The model presumes a constant event rate over time, an unrealistic assumption for many processes influenced by external factors, seasonality, or changing environmental conditions.
- Inaccurate Modeling of Trends: For processes where the event rate naturally increases or decreases, the Poisson model fails to capture this trend, leading to systematic prediction errors as the actual rate diverges from the assumed constant.
Real-Life Example: A retail store using Poisson Distribution to model customer arrivals ignores the effects of seasonality, like holiday rushes or summer lulls. The model’s assumption of a constant rate is violated, leading to inaccurate staffing levels, either being understaffed during peak times or overstaffed during slow periods, impacting profitability.
6. Simplistic Nature
The simplistic nature of Poisson Distribution can be a drawback in complex scenarios. It provides a basic model that does not account for the multifaceted aspects of real-world events. For instance, in healthcare, certain diseases might be influenced by genetics, environment, and lifestyle. The simplicity of Poisson Distribution means it might not capture these complexities adequately, leading to oversimplified and potentially misleading models.
This oversimplification limits its effectiveness in nuanced situations:
- Lack of Covariate Inclusion: The basic Poisson model cannot incorporate other explanatory variables (covariates) that might influence the event rate, failing to provide a comprehensive understanding of the factors driving the observed outcomes.
- Inability to Model Complexity: It is too simplistic for complex systems where events are influenced by multiple interacting factors, leading to an incomplete and often inaccurate representation of the underlying data-generating process.
Real-Life Example: Modeling the spread of an infectious disease with a simple Poisson model is inadequate. It ignores crucial factors like population density, vaccination rates, and social behavior. This oversimplification leads to poor predictions and ineffective public health policies, as it fails to capture the complex dynamics of disease transmission.
7. Ignoring Larger Context
Poisson Distribution focuses narrowly on the event count within a specified interval, often ignoring the larger context. This narrow focus can lead to overlooking broader trends or patterns crucial for accurate analysis. For example, in environmental studies, while Poisson Distribution can count the number of certain events, it may not account for underlying environmental changes or broader ecological systems that influence these events.
This myopic focus can result in a failure to see the bigger picture:
- Isolation of Events: The model treats events in isolation, ignoring the broader context or system in which they occur, which can be critical for understanding the true nature and drivers of these events.
- Neglect of External Factors: It fails to account for external influences or systemic patterns that may affect the event rate, leading to a model that is contextually blind and potentially missing key predictive information.
Real-Life Example: Counting the number of earthquakes in a region using Poisson Distribution ignores crucial geological context, like tectonic plate movements or aftershock sequences. This failure to consider the larger geophysical system can lead to inaccurate risk assessments and insufficient disaster preparedness plans for vulnerable populations.
8. Difficulty in Estimating Rate Parameter
Estimating the rate parameter (λ) in Poisson Distribution can be challenging, particularly when data is limited or events are extremely rare. This difficulty can lead to inaccuracies in the model, as the entire distribution hinges on the correct estimation of this parameter. In some fields, such as rare disease occurrences or uncommon natural phenomena, the scarcity of data can make the estimation of λ highly speculative and unreliable.
This challenge in parameter estimation undermines the model’s foundation:
- Data Scarcity Impact: Accurately estimating the rate parameter λ requires sufficient data. With rare events or limited observation periods, the estimate can be highly unstable and unreliable, compromising the entire model.
- Sensitivity to Parameter Error: The model’s output is highly sensitive to the value of λ. Small errors in its estimation can lead to large discrepancies in predicted probabilities, making the analysis fragile.
Real-Life Example: Estimating the rate of a rare industrial accident using Poisson Distribution is difficult due to limited historical data. The estimated λ might be based on only a few incidents, making it statistically unreliable. This can lead to either excessive safety spending or, worse, inadequate safety protocols.
9. Not Suitable for Large-Scale Data
Poisson Distribution may not be the best fit for large-scale data sets. In cases where data is extensive and complex, the distribution may fail to capture the nuances and intricate patterns present in the data. For instance, in big data applications, data’s sheer volume and complexity can render Poisson Distribution too simplistic, necessitating more sophisticated statistical models that can handle large-scale data more effectively.
Its simplicity becomes a liability when dealing with big data:
- Inability to Capture Complexity: Large-scale data often exhibits complex patterns, such as multiple modes or clusters, which the simple, single-parameter Poisson model is incapable of capturing and representing accurately.
- Computational Inefficiency: While simple in theory, applying Poisson models to massive datasets without accounting for their inherent structure can be computationally inefficient and may not leverage the full potential of the available information.
Real-Life Example: A large e-commerce platform analyzing user clicks across millions of sessions cannot rely on a simple Poisson model. The data’s scale and complexity, with varying user behaviors and patterns, require more advanced models like hierarchical or spatial Poisson processes to derive meaningful insights.
10. Exclusively Discrete Outcomes
A critical limitation of Poisson Distribution lies in its exclusive applicability to discrete outcomes. This distribution is designed to model the count of events, restricting its use to scenarios where outcomes are quantifiable in whole numbers. This characteristic significantly narrows its scope, particularly in fields where data is continuous or non-integer. In these cases, the discrete nature of Poisson Distribution renders it inadequate.
This restriction to discrete data limits its versatility across different fields:
- Inapplicability to Continuous Data: The model is exclusively for count data. It cannot be used to model continuous variables, such as measurements, weight, or temperature, which are common in many scientific and engineering fields.
- Limited Scope of Application: Its discrete nature confines its use to a specific subset of data types, making it an unsuitable choice for a wide range of statistical problems where continuous data is involved.
Real-Life Example: In finance, modeling the price of a stock, which is a continuous variable that can change by fractions of a cent, is impossible with Poisson Distribution. Using it would require inappropriate rounding of prices, losing critical information, and leading to flawed financial models and poor investment decisions.
Poisson Distribution Studies
Contemporary research continues to explore and refine the applications of Poisson Distribution and its extensions. Studies highlight both its enduring utility in specific contexts and the development of more robust models to address its limitations. The following resources provide a deeper dive into the theoretical underpinnings and practical applications of this important statistical tool.
- Poisson Distribution by ScienceDirect.com: A comprehensive overview of the theoretical foundations and applications of Poisson Distribution across various scientific disciplines.
- Poisson Distribution by Wikipedia.org: A detailed entry covering the mathematical properties, derivations, and related distributions, serving as a solid reference for students and researchers.
- An Extension of the Poisson Distribution: Features and Application for Medical Data Modeling: A research paper discussing advanced models that extend Poisson Distribution to better handle complexities like overdispersion in medical research.
Conclusion
While Poisson Distribution is a powerful tool in statistical analysis, its limitations cannot be overlooked. The ten disadvantages outlined in this article serve as a critical reminder that statistical models have specific conditions that must be met for accurate results. Misapplication can lead to erroneous conclusions and poor decision-making. As we’ve seen, its effective use requires a deep understanding of its constraints.
This awareness is vital for anyone applying statistical models. Recognizing the limitations of our tools is as important as understanding their strengths. Poisson Distribution remains a fundamental part of the statistical toolkit, but its application must be tempered with critical evaluation and a clear understanding of its underlying assumptions.
Suggested articles:
- Poisson Distribution: 5 Use Cases with 5 Advantages
- Top 5 Best Poisson Distribution Calculators
- Top 10 Cons & Disadvantages of Monte Carlo Analysis
Daniel Raymond, a project manager with over 20 years of experience, is the former CEO of a successful software company called Websystems. With a strong background in managing complex projects, he applied his expertise to develop AceProject.com and Bridge24.com, innovative project management tools designed to streamline processes and improve productivity. Throughout his career, Daniel has consistently demonstrated a commitment to excellence and a passion for empowering teams to achieve their goals.